§ Order and Degree

Order：Highest derivative
Degree：Highest power of the highest derivative

Example

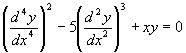
§ First Order D.E.

	Variable Separable	Homogeneous	Linear First Order
Pattern
Solving Technique	Separate x and y from both sides completely.	Let , then Yield	By integrating factor and the solution is
Further technique：Inspection (e.g. you should know xdy/dx + y is d(xy)/dx immediately) and Substitution

§ Typical Examples of First Order D.E.

Variable Separable：e.g. Rate of change of y is directly proportional to y.

Solution

=> => If initial condition t = 0, y = C0 is given, we have

Homogeneous：e.g. Fraction in Linear Polynomials (Can be converted into homogeneous type.)

Type A　A:B = D:E Coeffs. in proportion		Type B　A:B ≠ D:E Coeffs. not in proportion
Technique：Let u = Ax + By，convert the DE involves u and x only.		Technique：Let x = u + h，y = v + k，find h, k to convert the DE into DE involves u and v such that no constant terms occur in the fraction.
Example		Example
Solution		Solution
Let , then and the DE will be hence i.e.		Let , then ,and the DE will be , to make homo., set , having h = 2，k = －1, hence and the DE will be homogeneous, => Let , then , and DE will be hence 　(Partial fraction)

Linear First Order：e.g. Bernoull's Equation after suitable transformation.

Solve by the transformation of .

Solution

If , then , the DE will be => (Linear First Order) Integrating factor: The solution is 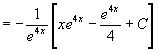Hence

§ Linear Second Order D.E.

Homogeneous：　　 (a, b, c are constants with a is non-zero)

Non-Homogeneous： (f(x) is non-zero function)

§ Solving Homogeneous Linear Second Order D.E.

Solve .

Step 1：Solve the auxiliary equation

Hence = ,

Step 2：Write down the solution according to the following three cases.
Distinct real roots ,	Equal roots = =	Complex roots , =
Solution：	Solution： or	Solution： or

§ Solving Non-Homogeneous Linear Second Order D.E.

Solve .

Step 1：Solve the homogeneous DE. Obtain the solution yc.

Solve by the method mentioned above and obtain the solution yc.

Step 2：Guess a particular solution yp by the method of undetermined coefficients.

By observing f(x), we can guess out yp easily in the following ways:

	f(x)	yp
Exponential
Polynomials
Sine and Cosine	or

Step 3：Modification for yp ?

If there is an expression in the guessing yp occurs in yc, just multiply the guessing yp by x. Continue this "multiplication process" until no term in yp occurs in yc.

Step 4：Substitute yp into the original DE to determine the coefficients in the yp.

Step 5：The general solution to the DE is y = yc + yp.

§ Typical Examples of Linear Second Order D.E.

Example 1：Solve .

Step 1：Solve

=> = 1, 2 => yc =

Step 2：Guess yp.

Since R.H.S. = ex, we guess yp = Cex.

Step 3：Modify yp.

Since ex occurs in yc, we need to modify yp as yp = Cxex.

Step 4：Determine coefficients in yp.

Let yp = Cxex, then and , substitute them back to the original DE, , hence C = 1, yield yp = xex.

Step 5：Write down the general solution y = yc + yp.

i.e.

Example 2：Solve .

Step 1：Solve

Step 2：Guess yp.

Beware! R.H.S. involves cos2x NOT cosx. We need to use . Hence the DE will be , thus .

Step 3：Modify yp.

Not necessary.

Step 4：Determine coefficients in yp.

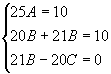, , sub. back to the original DE, we have =>, and =>

Step 5：Write down the general solution y = yc + yp.

i.e.

Example 3：Solve . (Hint: let .)

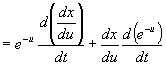
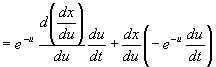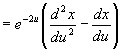
Try to convert the independent variable t into u through the transformation . Aim at writing 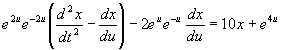, into something involves , . First of all, , hence . Now, and Substitute back to the original equation, we have --- (*) It's very easy to obtain . And it's trivial to guess , consequentially, and . Substitute into (*), , yield , thus ; therefore the general solution to the original DE is , i.e. .